Introduction

NOTE: Under construction. Very, very tentative! Also, the literature has not been searched for similar theories. This page only represents a theory. I have not PROVEN the claims below. I only suspect that they may be true and propose them for discussion. A proof or counter example may be fairly easy to come up with--I haven't given it time for either. Or, the facts may suggest that the theory must be fine-tuned. Regardless of the outcome, I think Cantor's Diagonal Argument should be useful in this subject--this is my main point. (It may also be useful in relation to other CLP languages like CLP(R) .)

In any event, I suspect that if the theory is correct, then someone has already proven it and stated more elegantly! (and recognized its possible relation to other Constraint Logic Programming languages). If you know of such literature, or have comments, your input would be most appreciated. This theory was inspired by, and naturally extents from, my graduate studies under Dr. Roger Cavallo and Dr. Jorge Novillo but I'm responsible for the thus-far half-baked aspect of this idea. I sometimes worry that when students have "ideas" they are really planted by their professors. (Intentionally sometimes, and at other times because professors occasionally cook up their ideas while teaching). To the extent that we student are correct in our "ideas", they are sometimes not really our own. (I learned about the beauty of invertibility in Dr. Novillo's Prolog class and first proposed the idea of this paper in a discussion in Dr. Cavallo's Special Topics class after Dr. Cavallo exposed me to Cantor's Diagonal Argument. The paper also reflects some concepts gained in Dr. Cavallo's Formal Methods class.)

Ideally, Prolog predicates should be invertible (except in rare cases for which instantiation testing is important.) Beautifully constructed invertible predicates are easily reused in programs and can be flexibly used in queries. You don't have to worry about the input-output assumptions that the programmer made. In its best, most fundamental form, you can think of Prolog not a functional language but rather as a relational language where arguments are not restricted to input or output roles. That's what I find to be so beautiful about Prolog. (And if you agree, I think that you will find the concept behind CLP(R) to be more attractive because Prolog often fall's short of what we may wish it to be. I haven't used CLP(R), but it looks great on paper and future CLP languages seem to have great potential.)

Unfortunately, from the code that I've seen, invertibility is rarely achieved. In my limited reading, I haven't seen a lot on the subject. So, here's a rather off-the-cuff attempt at furthering invertibility:

Theory of Invertibility

Let p be a Prolog predicate with arguments A¹, A², . . . Aⁿ , (each with denumerable¹ domains) where it is desired that p model a relation R.

Let Dⁱ be the domain (or should I say range when speaking of a relation, as opposed to a function?) associated with argument Aⁱ.

Let sⁱ be an element of the domain Dⁱ.

Provided that clauses of p make no test for instantiation² and provided that clauses of p execute only "fundamental"³ Prolog code:

If p is called with uninstantiated arguments and it happens that the sequence of solutions (outputted by Prolog) enumerates the state space {(s¹, s², . . . sⁿ)| p(s¹,s², . . . sⁿ)} (and no other states), then p is fully invertible⁴.

Note that I do not claim here that it is necessary that the solutions be instantiated. However, uninstantiated variables in the solution will not be so general as to "cover" space not covered by R (appropriately constrained) and will be general enough to cover the space covered by R subject to the constraints specified.

Example: two_ints. ("Two Integers"--Produces the possible pairs of positive integers.)

?two_ints_not_invertible(A,B).

A= 0 1 2 3 4 5 . . .
B= 0 0 0 0 0 0 . . .

If you call this predicate with an instantiated integer for argument B, you'll probably get a correct sequence of solutions. However, the sequence of solutions when called with uninstantiated arguments (shown above) indicates that this predicate might not be invertible. The sequence doesn't cover the state space of the relation. If we think in terms of Cantor's Diagonal Argument, we can see why:



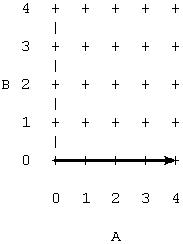
(It appears doubtful that this predicate will ever produce, for example, the solution A=2, B=2 if both A and B are uninstantiated. It is even questionable that the predicate will function properly if we call it with A=2 --it will probably generate the same sequence shown, skipping the first two states.)

?two_ints_invertible(A,B).

A= 0 0 1 0 1 2 0 1 2 3 . . .
B= 0 1 0 2 1 0 3 2 1 0 . . .

This predicate appears to be invertible. Again, we think in terms of Cantor's Diagonal Argument to show that the entire state space of the relation is "covered":

Summary

If the clauses of p make no test for instantiation, and it is proven that the sequence of solutions (for a predicate called with uninstantiated arguments) will be such that no solution will be missed, then p is invertible. A further requirement, for invertibility to be guaranteed, is that only "fundamental" code be employed--however, this requirement may be dropped or simplified in the future if the requirement is shown to be unnecessarily restrictive.

An unscientific rational for the theory might be expressed as follows: If a predicate can successfully enumerate its entire state space, it would appear that it could also enumerate a smaller portion of it. However as logical as that sounds, we know that we can, using tests for instantiation, make such a predicate fail under certain conditions. (For instance, we could program one of the above example predicates to fail if one argument is instantiated when the other is not.) For this reason, we require more than a Diagonal Argument for proof of invertibility.

Notes

1. Note that Cantor's Diagonal Argument proves that the reals are not denumerable. Invertibility probably cannot be guaranteed via this theory if reals or any other nondenumerable set constitutes the domain of an argument. (On the other hand, it may be constructive to note that reals are generally expressed on computers as finite numbers and that reals are always expressed in some finite fashion.)

2. Many built-in operators and predicates test for instantiation.

3. The term "fundamental" needs to be explained of course. A predicate that employs simple matching is an example of "fundamental" Prolog code. There are probably other examples of Prolog code that would qualify. An example of code that would not qualify as "fundamental" Prolog code would be any code that tests for instantiation. (More specifically, "unfundamental" code would at least include code that has the possibility of failing a goal due to the fact that an argument--or combination of arguments--was uninstantiated.) Of course, this leaves a lot of Prolog control operators and predicates to be properly categorized as "fundamental" or "unfundamental". "Fundamental" Prolog code is defined here as the operators or predicates for which this theory holds. Any proof of this theory might be constructed to prove (or disprove) the theory for one predicate at a time. However, a more general approach, broadly defining "fundamental" (with a proof for such a class of Prolog code), may be possible. I suspect that most (if not all) control operators will fail to fall in the "fundamental" class. I also suspect that data classification predicates will also fail to be "fundamental". In fact, I suspect, few Prolog constructs will qualify. (If this is frustrating, we may find ourselves rebuilding Prolog or exploring other CLP languages such as CLP(R).) However, an important point is that, with proper knowledge, many predicates can be beautifully constructed such that they are guaranteed to be invertible.

(It may be that when a predicate that makes no test for instantiation is "called" with uninstantiated arguments, and it happens that the sequence of solutions enumerate the solution state space intended to be covered by the predicate, then the predicate can be deemed invertible without having to check that the code is limited to "fundamental" constructs. This remains to be determined. For now, we will require "fundamental" code to be used, with the hope that we can ease invertibility insurance requirements in the future.)

4. By invertible I mean that the predicate may be "called" with any combination of instantiated and uninstantiated arguments resulting in a sequence of solutions (outputted by Prolog) that enumerates the state space appropriately constrained (or unconstrained) by the arguments. (The sequence of solutions will only "cover" the states that represent valid solutions, and will not "cover" any other states.) In addition, we require that invertible predicates eventually terminate once additional solutions are no longer possible.

Copyright 1996, David Lee Winston Miller. This document may be reproduced provided that it is duplicated in its entirety including all links, credits and copyright notices.

Resume

Homepage

Email